Lernauftrag 28: Belastungen im Drehstromsystem ermitteln

Hier findest du die Aufgaben ohne Lösungen.

In einem Wohngebäude sind folgende Wechselstromverbraucher an das Berliner TN-
Netzsystem angeschlossen:

• an L1: 1 Fernsehgerät \(230\ V/65\ W\); 1 Lampe \(230\ V/40\ W\)
• an L2: 1 Radio \(220\ V/10\ W\); 1 Toaster \(230\ V/300\ W\)
• an L3: 2 Lampen je \(230\ V/75\ W\)

Die Spannung an den Klemmen der Verbraucher wurde mit \(225\ V\) gemessen. Die Spannungsverluste über den Leitungen sollen vernachlässigt werden.

Aufgabe 1

Berechne die Ströme in den einzelnen Außenleitern und die Leistung, welche die Spannungsquelle abgibt.

L1

geg: \(U=225\ V, U_\mathrm{Nenn}=230\ V, P_1=65\ W, P_2=40\ W\)
ges: I
Lös:
\(R_1=\frac{(U_\mathrm{Nenn})^2}{P_1}=\frac{(230\ V)^2}{65\ W}=814\ \Omega\)
\(R_2=\frac{(U_\mathrm{Nenn})^2}{P_1}=\frac{(230\ V)^2}{40\ W}=1323\ \Omega\)
\(R_G=\frac{R_1\cdot R_2}{R_1+R_2}=\frac{814\ \Omega\cdot1323\ \Omega}{814\ \Omega+1323\ \Omega}=504\ \Omega\)
\(I_{\mathrm{L1}}=\frac{U}{R}=\frac{225\ V}{504\ \Omega}=0,44643\ A=446,43\ mA\)

L2

geg: \(U=225\ V, U_\mathrm{Nenn,1}=220\ V, P_1=15\ W, U_\mathrm{Nenn,2}=230\ V,P_2=300\ W\)
ges: I
Lös:
\(R_1=\frac{(U_\mathrm{Nenn,1})^2}{P_1}=\frac{(220\ V)^2}{10\ W}=4840\ \Omega\)
\(R_2=\frac{(U_\mathrm{Nenn,2})^2}{P_1}=\frac{(230\ V)^2}{300\ W}=176\ \Omega\)
\(R_G=\frac{R_1\cdot R_2}{R_1+R_2}=\frac{4840\ \Omega\cdot176\ \Omega}{4840\ \Omega+176\ \Omega}=170\ \Omega\)
\(I_{\mathrm{L2}}=\frac{U}{R}=\frac{225\ V}{170\ \Omega}=1,32\ A\)

L3

geg: \(U=225\ V, U_\mathrm{Nenn}=230\ V, P=75\ W\)
ges: I
Lös:
\(R_1=\frac{(U_\mathrm{Nenn})^2}{P}=\frac{(230\ V)^2}{75\ W}=705\ \Omega\)
\(R_G=\frac{R\cdot R}{R+R}=\frac{705\ \Omega\cdot705\ \Omega}{705\ \Omega+705\ \Omega}=353\ \Omega\)
\(I_{\mathrm{L3}}=\frac{U}{R}=\frac{225\ V}{353\ \Omega}=0,63739\ A=637,39\ mA\)

Leistung der Spannungsquelle

geg: \(I_1=446,43\ mA, I_2=1,32\ A, I_3, 637,39\ mA, U=225\ V\)
ges: \(P\)
Lös: \(P=U\cdot I=U\cdot(I_1+I_2+I_3)=225\ V\cdot(0,446\ A+1,32\ A+0,637\ A)=225\ V\cdot 2,403\ A=540,68\ W\)

Aufgabe 2

Bestimme zeichnerisch den Strom im Neutralleiter.

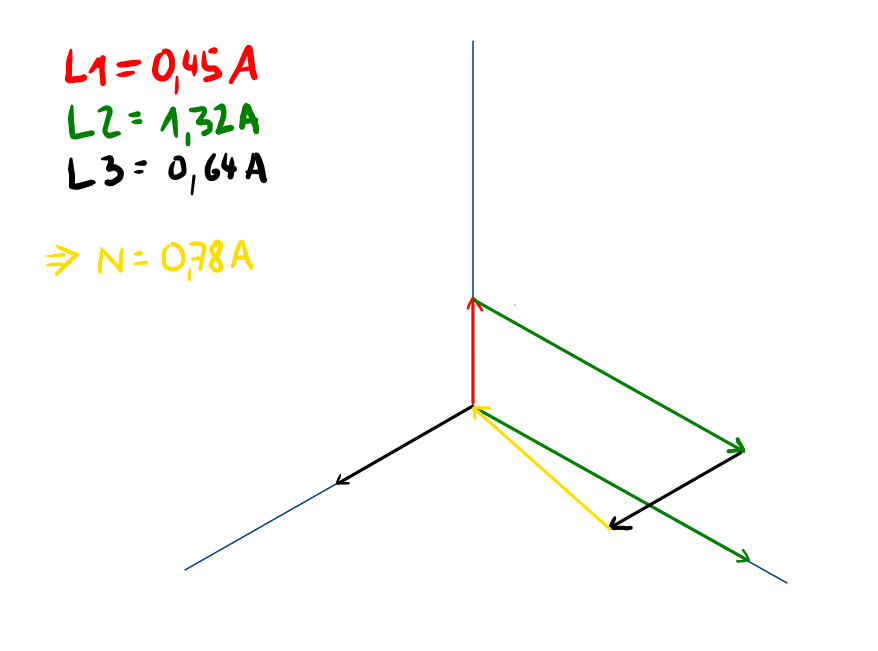
Aufgabe 3

Ein Durchlauferhitzer (DE) ist an einem Drehstromsystem 3/N/PE AC 50Hz \(400\ V\) angeschlossen. Die 3 Heizwiderstände haben jeweils einen Widerstand von \(20\ \Omega\). Die Schaltelektronik ist ausgefallen, so dass an Stelle der elektronischen Temperaturregelung eine mechanische Steuerung der Heizleistung in 3 Schaltstufen erfolgen soll.

Ein Lehrling hat dazu diese Idee:

Die Betriebsschaltung (Schaltstufe 3) ist die Dreieckschaltung.
Die Schaltstufe 2 wird durch Abschalten eines Außenleiters realisiert.
Durch Abschalten eines zusätzlichen 2. Außenleiters soll der DE in eine 1. Schaltstufe geschaltet werden.

Zeichne Ersatzschaltbilder für die drei Schalterstufen.

Stufe 3

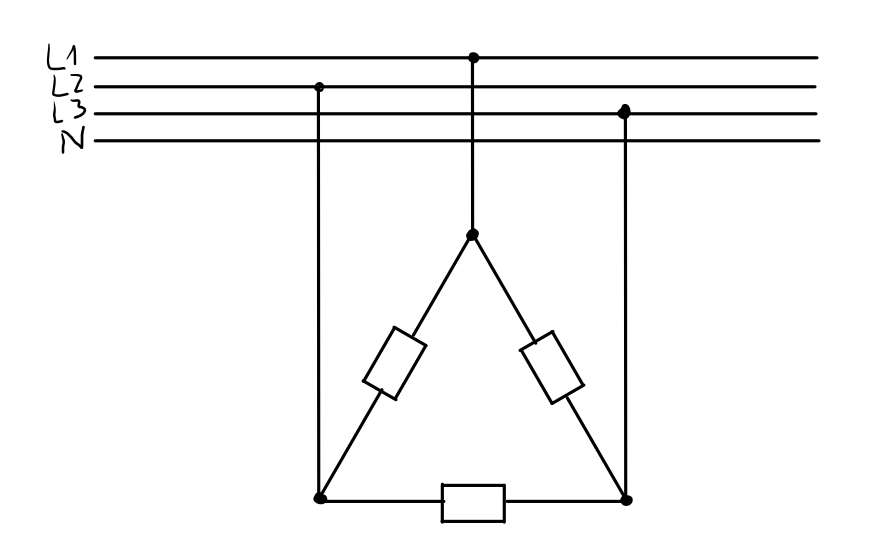
Stufe 2 (L1 getrennt)

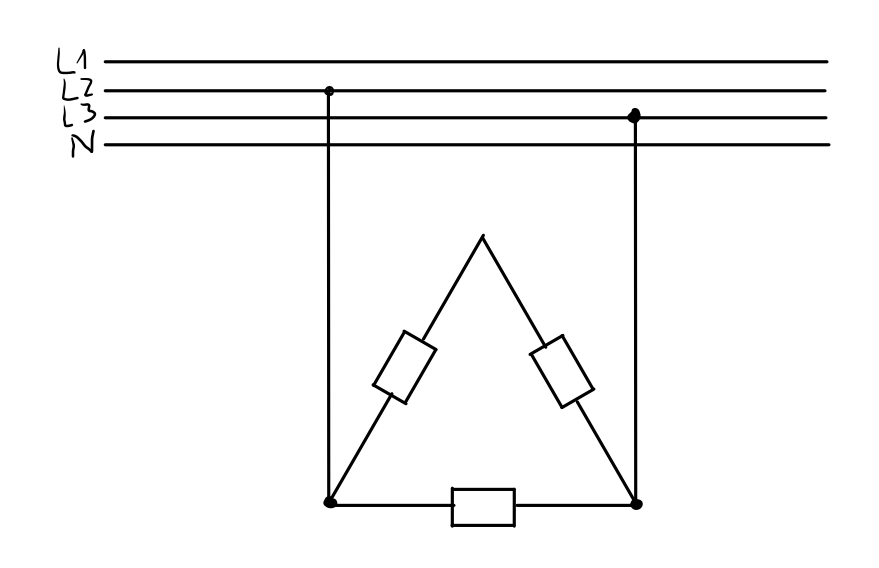
Stufe 1 (L1 + L2 getrennt)

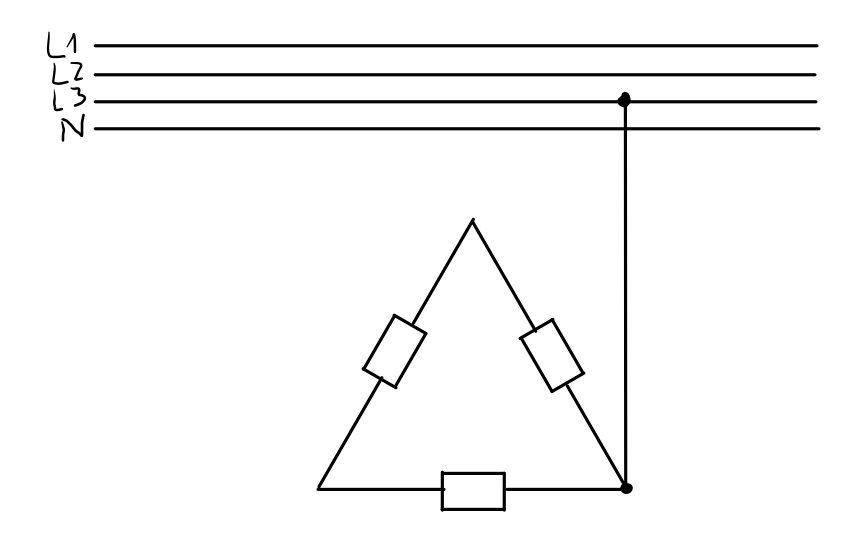
Aufgabe 4

Berechne für die drei Schalterstufen:

Leiterströme
abgegebene Leistung des Durchlauferhitzers

Stufe 3

geg: \(R=20\ \Omega, U=400\ V, \Delta\)-Schaltung
ges: \(I_\mathrm{L1}, I_\mathrm{L2}, I_\mathrm{L3}, P\)
Lös:
\(\Delta\)-Schaltung => \(U=U_\mathrm{Str}\)
\(I_\mathrm{Str1}=I_\mathrm{Str2}=I_\mathrm{Str3}=\frac{U_\mathrm{Str}}{R}=\frac{400\ V}{20\ \Omega}=20\ A\)
\(I_\mathrm{L1}=\sqrt{3}\cdot I_\mathrm{Str1}=\sqrt{3}\cdot 20\ A=34,6\ A\)
\(I_\mathrm{L2}=I_\mathrm{L3}=I_\mathrm{L1}=34,6\ A\)
\(P=\sqrt{3}\cdot U\cdot I=\sqrt{3}\cdot 400\ V\cdot 34,6\ A\approx24\ kW\)
Alternativ:
\(P=3\cdot U_\mathrm{Str}\cdot I_{Str}=3\cdot 400\ V\cdot 20\ A=24\ kW\)

Stufe 2

geg: \(R=20\ \Omega, U=400\ V, \Delta\)-Schaltung
ges: \(I_\mathrm{L2}, I_\mathrm{L3}\)

Zuerst einmal ein Ersatzschaltbild, damit wir die Situation besser verstehen:

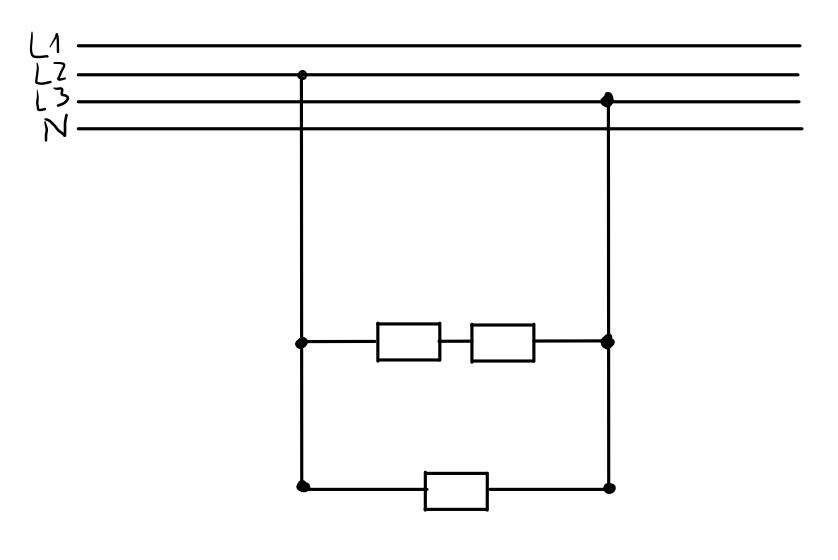
Offensichtlich haben wir nun nur noch einen Wechselstromkreis. In diesem sind zwei parallele Stränge, einmal mit einem, einmal mit zwei Widerständen. Um den Leiterstrom zu finden, müssen wir diese zuerst zusammenfassen.

Die Widerstände in Reihe ersetzen wir durch:
\(R_1=R+R=20\ \Omega+20\ \Omega=40\ \Omega\)

Die Parallelschaltung aus \(R\) und \(R_1\) ersetzen wir durch:
\(R_\mathrm{ges}=\frac{R\cdot R_1}{R+R_1}=\frac{20\ \Omega\cdot 40\ \Omega}{20\ \Omega+40\ \Omega}=13,33\ \Omega\)

\(I=\frac{U}{R}=\frac{400\ V}{13,33\ \Omega}=30,1\ A\)
\(P=U\cdot I=400\ V\cdot 30,1\ A\approx12\ kW\)

Stufe 1

kein geschlossener Stromkreis => Leiterströme Null => Leistung Null

Aufgabe 5

Bewerte, ob diese Steuerung sinnvoll ist.

Die Steuerung ist nicht sinnvoll, da in Stufe 1 der Herd nach wie vor ausgeschaltet ist.